Benaderingen van pi. François Viète.
Viète is de eerste die \({\pi}\) heeft weergegeven als resultaat van een oneindig product. Hij gebruikte daarbij de zogenaamde uitputtingsmethode en begon met het vierkant als eerste regelmatige veelhoek. De oppervlakte van dit vierkant in de eenheidscirkel (r=1) is \({\sqrt2 \times \sqrt2 = 2}\).
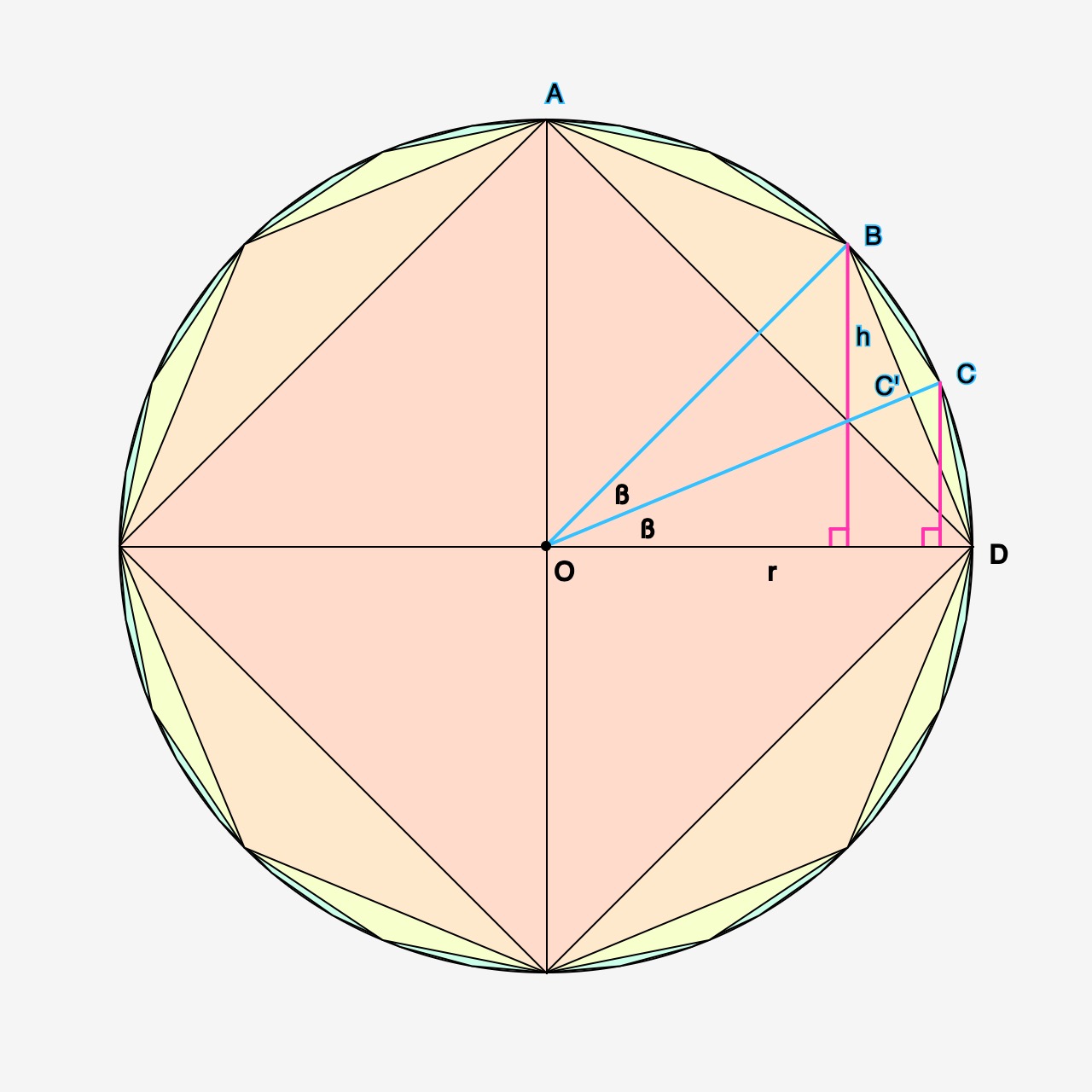
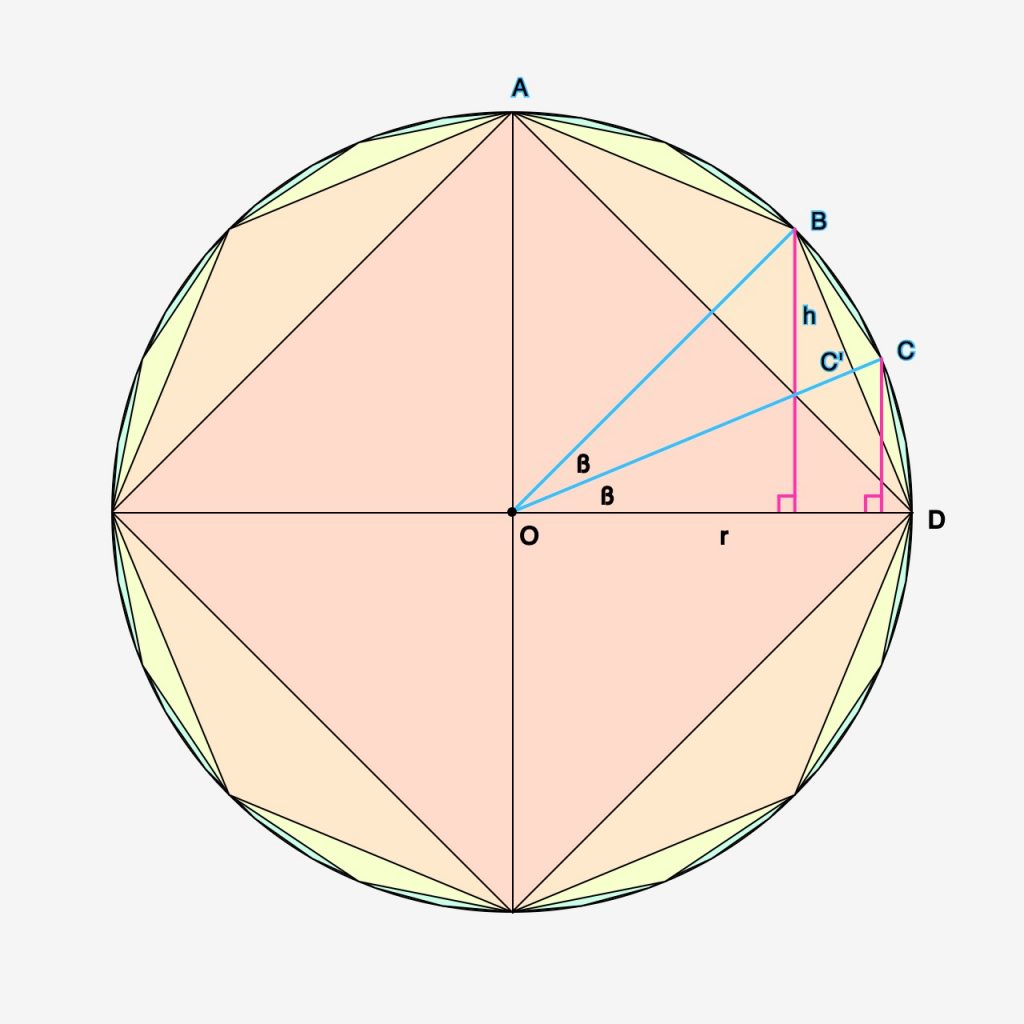
De oppervlakte van een veelhoek kan ook worden berekend aan de hand van de samenstellende driehoeken. Bij het vierkant zijn dat er 4; we nemen dus n=4. De oppervlakte van een driehoek is basis (OD) keer hoogte (OA) gedeeld door 2. Van \({\bigtriangleup OAD}\) is dat eenvoudig: \({{{1 \times 1} \over 2}= {1 \over 2}}\). Omdat n=4 is de oppervlakte dus 2.
De kernvraag
De oppervlakte van \(\bigtriangleup OBD ={{OC’ \times BD} \over 2} \). De lengte van OC’ is \(cos(ß) \cdotp r\); de basis BD heeft lengte \({sin(ß) \cdotp r}\times 2\). Dus $$ \bigtriangleup OBD ={ {{cos(ß) \cdotp r} \cdotp {{sin(ß) \cdotp r} \times 2}\over 2} }={r^2 \cdotp cos(ß) \cdotp sin(ß)}$$
De oppervlakte van OBCD is 2 keer \({\bigtriangleup OCD}\) (basis OD keer hoogte (loodlijn uit C) gedeeld door twee), dus \( {{{sin(ß) \cdotp r \cdotp r}\over 2 } \times 2}\) wat vereenvoudigt neerkomt op \( {sin(ß) \cdotp r^2}\) .
Berekening van de driehoeken
Noemen we \({\bigtriangleup OBD}\) \({A_{n}}\) en OBDC \({A_{2n}}\) dan ziet de groeifactor er als volgt uit: $${{A_{2n}\over A_{n}}={{ r^2sin(ß)}\over { r^2sin(ß)cos(ß)}}={1 \over cos(ß)}}$$ Met andere woorden: de toename van de oppervlakte van het vierkant naar die van de achthoek is afhankelijk van de cosinus van de in tweeën gedeelde hoek, In het geval van het vierkant is dat dus de \(cos(45^{\circ})= {\sqrt 2 \over 2}\). Dus \( A_8=2 \cdotp {2 \over \sqrt 2} \)
De groeifactor voor de volgende veelhoek
Deze procedure kunnen we nu herhalen voor \(A_{2n}\) en \(A_{4n}\) met als hoek \({ß \over 2}\). Dan is \(A_{2n}=r^2sin({ß \over 2})cos({ß \over 2})\) en \(A_{4n}=r^2sin({ß \over 2})\). De groei van \({A_{2n}}\) naar \({A_{4n}}\) is $${{A_{4n}\over A_{2n}}={{r^2sin({ß \over 2})}\over {r^2sin({ß \over 2})cos({ß \over 2})}}={1 \over cos({ß \over 2})}}$$
Dus $${A_{4n}\over A_{n}}={A_{2n}\over A_{n}} \times {A_{4n}\over A_{2n}}={1 \over {{cos(ß) \times cos({ß \over 2})}}}$$
Waarom gebruikten we n, 2n en 4n? Om de hoek ß te relateren aan het aantal hoeken van de veelhoek en uit te drukken als verhouding van pi en n. We zijn begonnen met n=4 en telkens verdubbelen we het aantal hoeken: n, 2n, 4n, 8n etc. Bij n: \(ß={{ \pi \over 4}={45^{\circ}}}\). Dus voor ß kunnen we nu \(\pi \over n \) invullen): $${A_{4n}\over A_{n}}={A_{2n}\over A_{n}} \times {A_{4n}\over A_{2n}}={1 \over {{cos({{ \pi} \over n}) \times cos({{ \pi} \over 2 \cdot n})}}}$$
Uitbreiding naar pi
Neemt het aantal hoeken van de veelhoek toe dan zal de oppervlakte ervan steeds dichter bij de oppervlakte van de cirkel komen:$$\ \lim_{k\to \infty} A{_{(2^kn)}\cdotp r^2}=\pi r^2$$
$${A_{{(2^kn)}} \cdot r^2 \over {A_n\cdot r^2} }={\pi \cdot r^2 \over A_n \cdot r^2 }=
{1 \over {cos({ \pi \over n})
\cdotp {cos({{ \pi} \over 2n})
\cdotp … cos({{ \pi} \over {2^kn}}
)}}}$$
Het resultaat na vereenvoudiging en met \({k \to \infty}\) en n=4:
$${\pi = {A_n \over cos({ \pi \over n}) \cdotp …\cdotp cos({{ \pi} \over {2^kn}
})}={2 \over cos({ \pi \over 4}) \cdotp …\cdotp cos({{ \pi} \over {2^k4}
})}}$$
De magie: toepassing van de halvehoek formule
Door de halvehoek formule kunnen de cosinussen worden weergegeven als soort herhaalrecept van de hoek waarmee is begonnen: $${cos({\theta \over 2})}=\sqrt {{1 \over 2} + {1 \over 2 } \cdotp cos( \theta)}$$
De formule voor \(\pi\) kunnen we dus als volgt herformuleren (n=4 en \({cos({\pi \over 4})}={\sqrt {1 \over 2}}\)): $$ \pi = {2 \over {\sqrt {1 \over 2}} \cdotp{\sqrt {{1 \over 2} + {1 \over 2 } \cdotp \sqrt {1 \over 2}} } {\cdotp \sqrt {{1\over 2}+ {{1 \over 2} \sqrt{{1 \over 2}+{{1 \over 2} \sqrt{1 \over 2}}}}}\cdotp …… }} $$
Willen we \(\pi\) benaderen met behulp van de groeifactor, zoals we hierboven als hebben gedaan voor \(A_8\) en \(cos({\pi \over 4})= {\sqrt 2 \over 2}\) dan ziet de benadering er voor het oog iets aangenamer uit:
$$ \pi =2 \cdotp {2 \over \sqrt 2}
{\cdotp {2 \over \sqrt {2 +\sqrt 2}}}
{\cdotp {2 \over \sqrt {2 +\sqrt {2 +\sqrt 2}}}} ……
$$
Als “Vièta’s formule” worden de wortels in de teller geplaatst: $$ {2\over \pi} ={\sqrt 2 \over 2}{\cdotp { \sqrt {2 +\sqrt 2}\over 2}}{\cdotp {{\sqrt {2 +\sqrt {2 +\sqrt 2}} \over 2}}} ……$$
Dit is in essentie de benadering van pi die Viète in 1593 heeft gepubliceerd in zijn Variorum de rebus mathematicis de responsorum liber VIII. (hier in versie gepubliceerd in 1593. Ter verduidelijking: Een binomium is een getal dat niet verder te vereenvoudigen is, bv \(12 +\sqrt 11\) In Viètes oospronkelijke tekst staat Radix binomia 2 -> radice 2 gelijk met \(\sqrt {2 + \sqrt2}\)) De uitputtingsmethode die Viète hanteerde en uitmondde in de weergave van pi als een oneindige voortzetting van dezelfde bewerking was niet nieuw. Wel nieuw was de manier waarop Viète het idee uit de Griekse geometrie met de nieuwere algebraïsche middelen te lijf was gegaan. Daardoor hij kon deze benaderingswijze in een kwantitatieve vorm gieten met \({\pi}\) als resultaat van een oneindige vermenigvuldiging. De vraag hoe dat precies zou aflopen stelde Viète niet. Zou het werkelijk convergeren of zou het op de drempel van oneindigheid toch misschein net mis gaan.
Toen Cantor in een bespreking van Das Problem von der Quadratur des Zirkels van F. Rudio had opgemerkt dat hij graag een bewijs zou zien dat Viète’s benadering daadwerkelijk naar \({\pi}\) convergeert, heeft Rudio de uitdaging opgepakt en in een brief aan Cantor het bewijs geleverd. Het is gepubliceerd in1891 in het Zeitschrift für Mathematik und Physik.