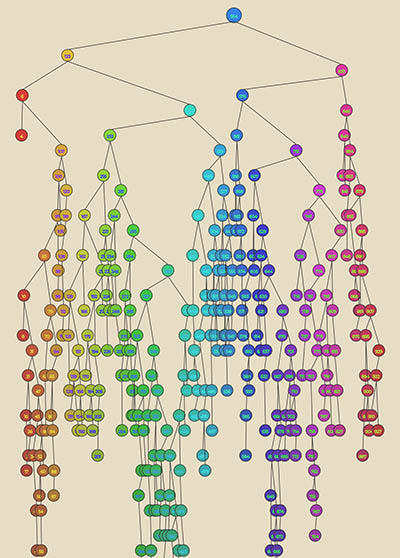
De Calder Zoekboom

Alexander Calder (1898-1976) maakte sculpturen die bekend zijn geworden onder de naam die Marcel Duchamp eraan heeft gegeven: mobielen. Ze hingen aan plafonds of waren onderdeel van een andere sculptuur, zoals in Laocoön uit 1947. Aan de met elkaar verbonden dragers hingen meestal één of twee blaadjes, soms gekleurd, soms niet. Door de manier van ophangen heeft de wind vrij spel. Bij een zuchtje wind komen de sculpturen in beweging en dansen in het rond. Hoe ze er exact uit zien wordt dus mede bepaald door het toeval.

Calder zal het wel nooit geweten hebben, maar zijn kinetische sculturen zijn prachtige illustraties van wat in de computerwereld een Binary Search Tree of een Binaire Zoekboom wordt genoemd. Iedere knoop (node) in de boom verwijst naar twee andere knopen waarbij de ene knoop een sleutelwaarde heeft die kleiner is dan zijn “ouder” en de andere een waarde die groter dan zijn “ouder” is. Dus elke knoop verdeeld de wat onder de knoop komt, de subboom, in tweeën: aan de ene kant zijn alle waardes kleiner en aan de andere zijde zijn alle waardes groter.
Informatie wordt in een zoekboom opgeslagen omdat het terugvinden ervan met behulp van de sleutel efficiënt verloopt: bij elke stap wordt het aantal knopen dat moet worden doorlopen de helft kleiner -als de zoekboom tenminste gebalanceerd is.

In het Oinou mobiel hieronder kunnen de eigenschappen van de binaire zoekboom worden verkend. Een verandering van elk van de twee schuiven maakt een nieuwe boom: de bovenste schuif vergroot het getal waaruit gerandomiseerd wordt gekozen en de tweede schuif bepaalt het aantal knopen van de boom.
Heb je een boom die je mooi vindt dan ga je er mee experimenteren. Knopen toevoegen of knopen vinden kan door in het invoervakje rechts een getal in te typen en dan op de knop “Vind node” of “Node invoegen” te klikken. Een knoop verwijderen kan door eerst de knoop met een klik erop te selecteren en dan op de knop Verwijderen te klikken.

Laten we nog éé keer terugkijken naar wat Alexander Calder in 1932 heeft gemaakt en genieten van wat we nu the art of the binary tree noemen.