Benaderingen van pi. Recursie

Laten we er eens op een andere manier naar kijken dan we in de vorige aflevering hebben gedaan. De uitputtingsmethode die Viète hanteerde en uitmondde in de weergave van \({\pi}\) als een oneindige voortzetting van dezelfde bewerking was bepaald niet nieuw. Wel nieuw was de manier waarop Viète dit idee uit de klassieke geometrie met de nieuwe algebraïsche middelen had uitgewerkt. Daardoor hij kon deze benaderingswijze in een kwantitatieve vorm gieten met \({\pi}\) als resultaat van een oneindige vermenigvuldiging.
De vraag of het werkelijk zou convergeren of op de drempel van oneindigheid toch misschein net zou mis gaan, stelde Viète niet. In 1891 heeft een zekere F. Rudio bewezen dat deze aanpak daadwerkelijk naar \({\pi}\) convergeert.

Maar hoe kunnen we het repeterende, het recursieve van deze benadering meer naar voren halen? Door het resultaat R weer te geven als het resultaat van een bewerking B (de verdubbeling van het aantal hoeken of de halvering van de hoek) waaruit R zelf is ontstaan: \(R_n=B(R_{n-1})\).

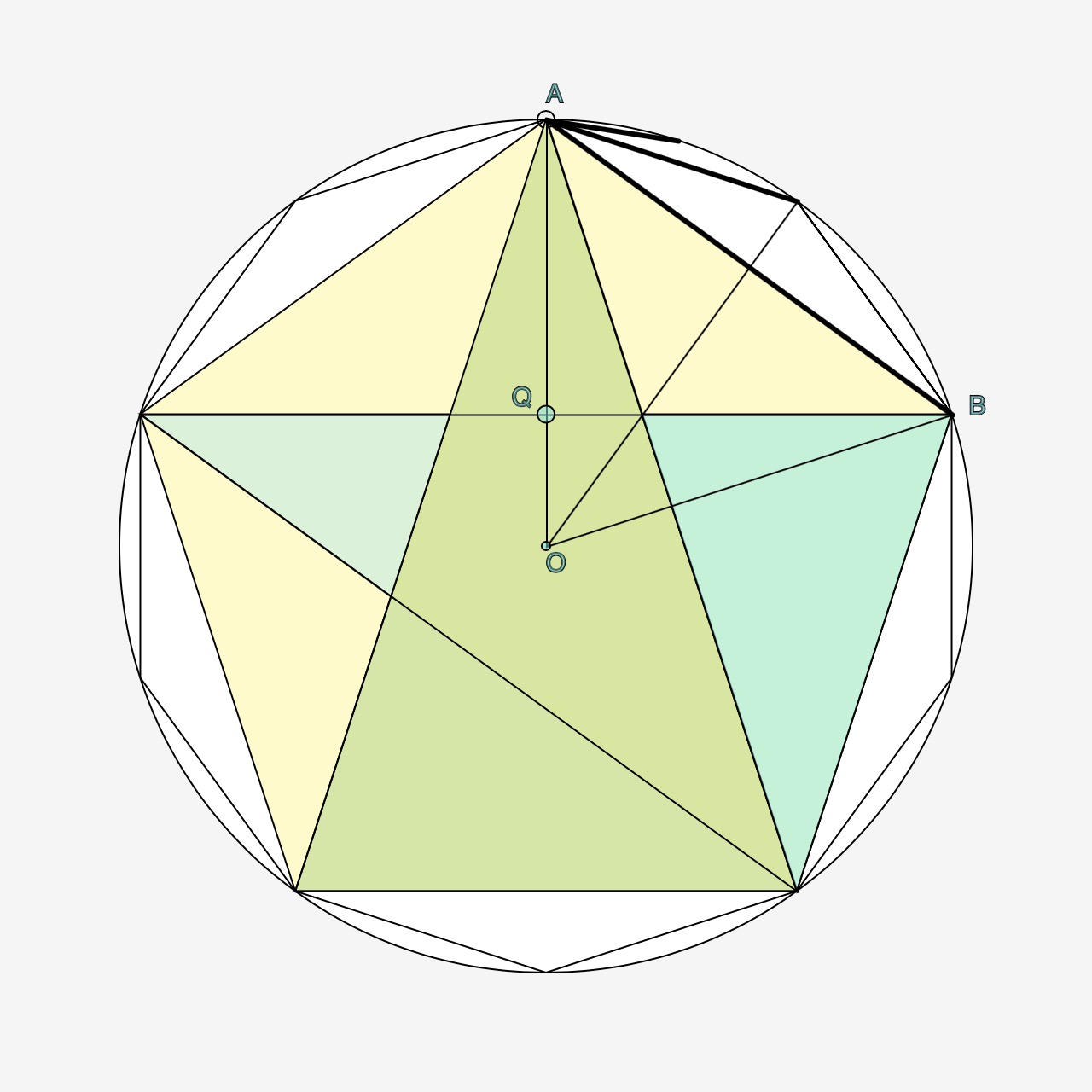
In figuur 1 nemen we A als uitgangspunt en kijken naar de hoek die bij een verdubbeling van de veelhoek ontstaat tussen de nieuwe zijde uit A en de zijde uit A van de vorige veelhoek. \(\angle BAD \) is de helft van \(\angle DAO \) en dat herhaalt zich in A voor alle daarop volgende veelhoeken. Dus als \(\angle DAO \) gelijk is aan \(\pi \over 4\) dan is \(\angle BAD \)  \(\pi \over 8\).
Algemeen gesteld met n als aanvangsveelhoek (bv. 3, 4 of 5) en k=0,1,2,3,4,….: bij veelhoek \(2^k n\) is de nieuwe hoek \(\pi \over {2^kn}\).

Werken een concrete situatie uit voor n=4 en k=0. In dit geval gaat het dus om zijde AB, die net iets groter wordt dan AE: $$AB={{1 \over cos({\pi \over {2^kn}})} \times AE} $$ Omdat AE de helft is van de zijde van de vorige veelhoek geldt dus: \(AE={{1 \over 2 } \cdot AD}\) . We kunnen nu de nieuwe zijde Z als volgt bepalen:
$$Z_{2^kn}={{1 \over cos({\pi \over {2^k}n})} \times {{1 \over 2} \cdotp Z_{{2^{k-1}n}}}}$$ Vereenvoudigd: $$Z_{2^kn}={{{ Z_{{2^{k-1}n}}} \over 2 \cdotp cos({\pi \over {2^k}n})} }$$
Maar laten we eens goed kijken naar \(2 \cdotp cos({\pi \over {2^k}n})\). Met de halvehoek formule kunnen dit onderdeel ook recursief vereenvoudigen en terugbrengen naar de starthoek \(\pi \over n\) als k=0. Laten we het de deelfactor F noemen: \(F_n=2 \cdotp cos({\pi \over n})\). De volgende deelfactor is[ref]We hebben 2 als \(\sqrt 4\) genomen en vermenigvuldidgt met de andere wortel \(\sqrt 4 \cdotp {\sqrt {{1\over 2}+{1 \over 2}cos({\pi \over n})}}\). Dus: \(\): \(\sqrt { 2+ 2 \cdotp cos({\pi \over n})}\)[/ref] $$F_{2n}=2 \cdotp cos({\pi \over 2n})\\=2 \sqrt{{1 \over 2}+ {{1 \over 2} \cdotp cos({\pi \over n})}}\\=\sqrt{2 + F_n}$$Het resultaat van deze overpeinzing is dus dat $$F_{2^kn}=\sqrt{2 + F_{2^{k-1}n}}$$
Met dit resultaat kunnen we de recursie voor de zijde Z algemeen formuleren (waarbij geldt \(F_{n}=2 \cdotp cos({\pi \over n})\) ):
$$Z_{2^kn}={{{ Z_{{2^{k-1}n}}} \over \sqrt{2 + F_{2^{k-1}n}} }}$$
Voor de omtrek O van een veelhoek moet we de lengte van de zijde vermenigvuldigen met het aantal hoeken: \({2^{k}n}\): $$O_{2^kn}={{{ Z_{{2^{k-1}n}}\cdotp {2^{k}n}} \over \sqrt{2 + F_{2^{k-1}n}} }}$$ De omtrek zal, naarmate k toeneemt, steeds dichter bij de omtrek van de cirkel, \(2 \pi\) komen te liggen: $$ \lim_{k\to \infty} O_{2^kn}={2 \pi}$$

Delen we dit resultaat door twee dan kunnen we \(\pi\) als volgt definiëren: $$ \pi=\lim_{k\to \infty}{{{ Z_{{2^{k-1}n}}\cdotp {2^{k-1}n}} \over \sqrt{2 + F_{2^{k-1}n}} }}$$

Praktische uitwerkingen.

Benadering vanuit het vierkant

Nemen we n=4 en k=1. Dan is \(F_4=2cos ({\pi \over 4})=2 \cdotp{ {1 \over 2} \sqrt 2}=\sqrt 2\) en zijde \(Z_8\)$$ {\sqrt 2 \over  {\sqrt {2 + \sqrt 2}}} $$
De volgende stap, k=2:
$$Z_{16}={ {\sqrt 2 \over {\sqrt {2 + \sqrt 2}}} \over  \sqrt {2 +\sqrt {2 +\sqrt 2}}}={ {\sqrt 2 \over {{\sqrt {2 + \sqrt 2}}} \cdot \sqrt {2 +\sqrt {2 +\sqrt 2}}}}$$

Benadering vanuit de driehoek

We kunnen natuurlijk ook beginnen met een driehoek waarbij \(F_3=2cos ({\pi \over 3})=2 \cdotp{ {1 \over 2}}=1\) en n=3.
De eerste twee stappen (k=0 en k=1)zijn dan:
\(Z_3= \sqrt 3 \)
\(Z_6={\sqrt3 \over \sqrt {2+ 1}}={\sqrt3 \over \sqrt 3}=1\).
\(Z_{12}\) laat zich nu gemakkelijk berekenen en hoe de structuur zich voortzet wordt duidelijk aan \(Z_{24}\) waarbij k=3.

$$Z_{12}={1 \over {\sqrt {2 + \sqrt 3}}}$$
$$Z_{24}={{1 \over {\sqrt {2 + \sqrt 3}}} \over {\sqrt {2+\sqrt {2 + \sqrt 3}}}}={{1 \over {\sqrt {2 + \sqrt 3}} \cdotp {\sqrt {2+\sqrt {2 + \sqrt 3}}}} }$$

Benadering vanuit de vijfhoek

Met deze benadering komt er iets nieuws in het spel, namelijk de gulden snede, ook aangeduid met \(\phi\). Dat gaat als volgt[ref]Want \(\phi={{1+\sqrt 5} \over 2}\)[/ref] : $${cos({\pi \over 5})}={{1+\sqrt 5} \over 4}\\={\phi \over 2}$$
Nu we dit weten kunnen we schrijven: \(F_{5}=2 \cdotp cos({\pi \over 5})=\phi\)

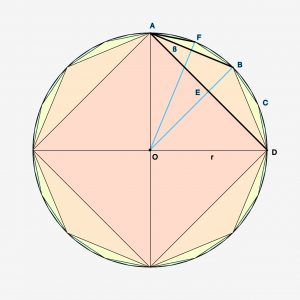
Maar hoe vinden we de lengte van één van de vijf zijdes? De regelmatige vijfhoek is op te delen in drie driehoeken die het volledig uitvullen. Dus dat levert samen aan hoeken \(3 \pi\) op. Elk van de vijf hoeken is dus \({3 \pi \over 5}={108 ^\circ}\). De hoek OAB is dus de helft van \(108 ^\circ\) is \(54 ^\circ\). De hoek ABQ is \(90 ^\circ -54 ^\circ =36 ^\circ\). Omdat driehoek OAB gelijkbenig is is hoek ABO even groot als OAB. Hoek OBQ is derhalve \(54 ^\circ -36 ^\circ =18 ^\circ\).
De lengte van OB is \( {cos({\pi \over 10})}={{1 \over 4} \sqrt{10 + 2 \sqrt5}})\).
De lengte van AQ is \( 1-sin({ \pi \over 10})= 1-({1 \over 4} \sqrt 5 -{1 \over 4})\).
Met Pythagoras kunnen we AB berekenen. Het kwadraat levert de volgende berekening: $$({{1 \over 4} {\sqrt{10 + 2 \sqrt5}}}) ^2 +{({5 \over 4}-{ {1 \over 4}\sqrt 5})^2} $$ Het resultaat is $$ AB={\sqrt {10 – 2\sqrt 5} }$$
Wat is nu de lengte van volgende stap? Dat is \({\sqrt {10 – 2\sqrt 5} }\) gedeeld door \(\sqrt {2+\phi}\) (wat gelijk is aan \(2 \cos({\pi \over 10})\) = \({1 \over 2} \sqrt {10 + 2\sqrt 5}\))$$ Z_{10}={{\sqrt {10 – 2\sqrt 5} }\over{{1 \over 2} \sqrt {10 + 2\sqrt 5}}}={{\sqrt {10 – 2\sqrt 5} }\over \sqrt {2+\phi}}={{\sqrt 5 -1}}={2\over \phi}$$
De volgende is $${Z_{20}}={{2 \over \phi} \over \sqrt {2 + \sqrt{ 2 +\phi}}}\\={{2} \over {\phi} \cdotp \sqrt {2 + \sqrt{ 2 +\phi}}}$$  De volgende zijde wordt dan volgens de bekende regel: $${Z_{40}}={2 \over \phi \cdotp \sqrt {2 + \sqrt{ 2 +\phi}} \cdotp \sqrt {2 + \sqrt{ 2+ \sqrt {2 +\phi}}} }$$

 

 

 

link golden ratio