Euclides’ constructie van een middelevenredige lijn

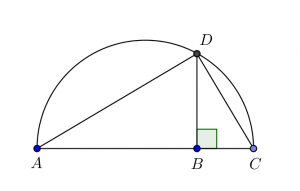
Euclides laat in Boek VI propositie 13 zien hoe een middelevenredige lijn kan worden geconstrueerd tussen de lijnen AB en BC. Leg AB (a) en BC (b) in elkaars verlengde. Trek vanuit B een loodlijn. De cirkel met straal AC/2 snijdt de loodlijn in D. BD (x) is de gezochte middelevenredige lijn tussen AB en BC.

De middelevenredige lijn is dus de zijde van een vierkant dat een oppervlakte heeft die even groot als de oppervlakte van de rechthoek met zijdes AB (a) en BC (b). Algebraïsch laat middelevenredigheid zich als volgt formuleren: a:x=x:b; dus x² = ab of x = √ab.

Computerconstructie van middelevenredige lijnen

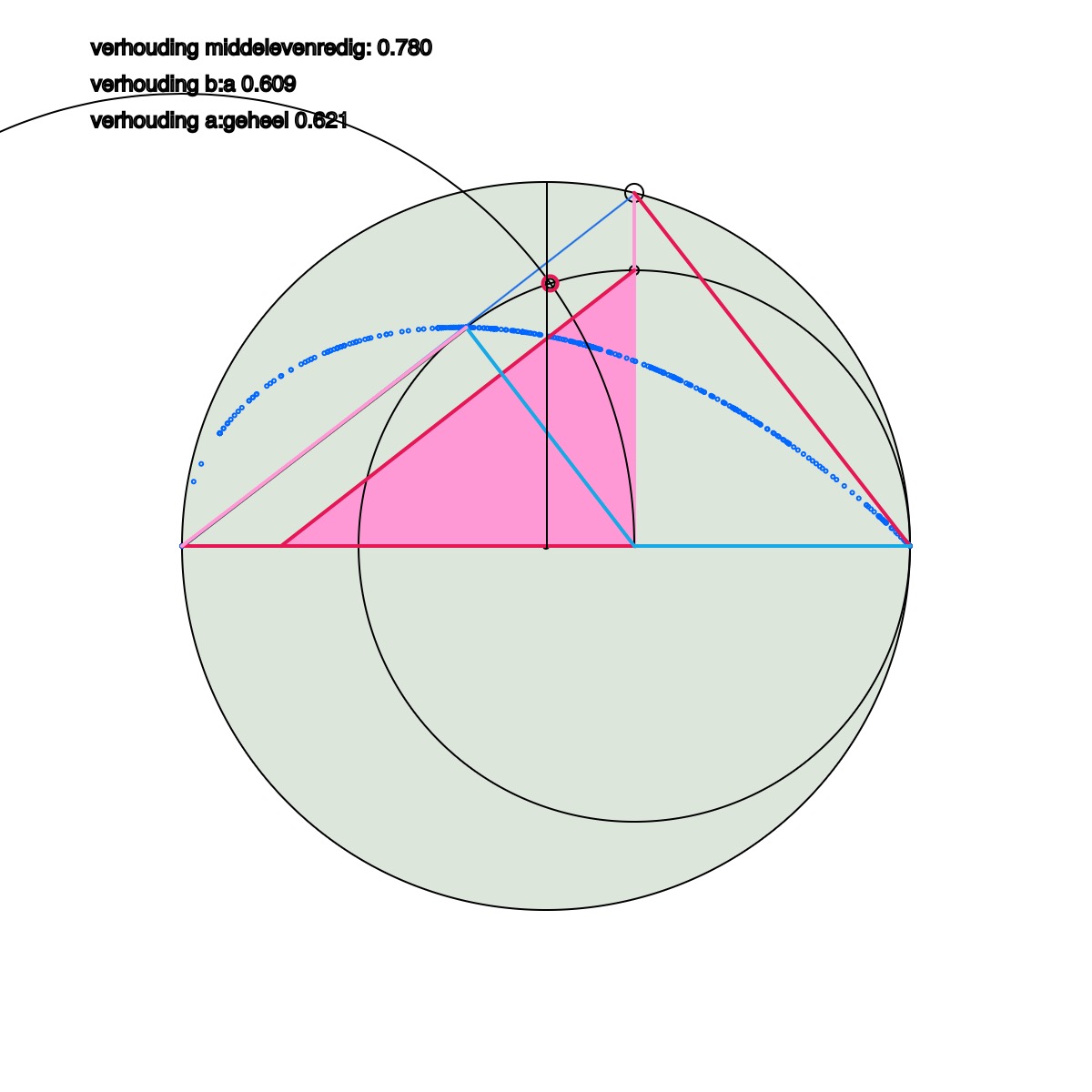
Met de computer kunnen we heel gemakkelijk een veelheid van middelevenredige lijnen construeren. Afhankelijk van de positie van de muis (van rechtsboven naar linksonder) beweegt zich C over de uitgangscirkel, ontstaat de rechthoekige driehoek ABC en wordt de diameter verdeeld in a en b .

Euclides geometrische midden

Middelevenredigheid en de gulden snede

Er zal dus ook een positie van C zijn waarbij de diameter van de cirkel overeenkomstig de gulden snede wordt verdeeld. Dan geldt b: a = a : a+b, dus ab=a²-b². Omdat zoals we zojuist zagen ab = x² kunnen we nu ook schrijven x²=a²-b² of x²+b²=a². Dit is de fameuse stelling van Pythagoras maar dan onder de voorwaarde dat de hypothenusa (a) en de korte rechthoekszijde (b) zich verhouden als de gulden snede (en x dus middelevenredig tussen a en b is). Hoe vind je deze driehoek?

Middelevenredige Gulden Snede

Trek een cirkel met straal b op het snijpunt van de middelevenredige lijn (x) en de diameter. Trek vanuit A een lijn tangentieel aan deze cirkel, noem het raakpunt G. De straal GE staat loodrecht op tangens AG.
Als de hoek GAE gelijk is aan hoek CAB verdeelt x de diameter in een gulden snede!1 In dit geval ontstaan drie gelijke driehoeken: ∇AEG, ∇DEF en ∇EBC. Hoek GEA is gelijk aan hoek CBE. In dit geval is CB even groot als AE (a). Voor ∇EBC geldt nu x²+b²=a²; met andere woorden de combinatie van gulden snede en middelevenredigheid.

Keplers driehoek

Deze combinatie was Johannes Kepler al op het spoor. Hij schreef in 1597 aan zijn professor Mästlin: “If on a line which is divided in extreme and mean ratio2 one constructs a right angled triangle, such that the right angle is on the perpendicular put at the section point, then the smaller leg will equal the larger segment of the divided line.” Wat Kepler zegt is dat als AB in E wordt verdeeld volgens de gulden snede en de rechte hoek C exact boven dit punt komt te liggen dat dan AE en BC gelijk zijn.

Het bijzondere van deze driehoek is dat de zijden zich laten uitdrukken met behulp van phi, de gulden snede ratio. Stellen we \(EB=1\), dan geldt \(x=\sqrt \phi\) en \(BC=\phi\) met als resultaat een bijzondere versie van de stelling van Pythagoras: \(\phi^2=\phi +1\).

Bewijs dat AB door CE in verhouding van gulden snede wordt verdeeld

Als de cirkel met als centrum E en straal EB de cirkel met centrum A en straal AE elkaar snijden op een punt dat exact boven het centrum van de uitgangscirkel ligt, dus OO’ snijdt, dan verdeelt E AB exact in verhouding van de gulden snede.
Middelevenredige Gulden Snede

De x-waarde van het snijpunt van twee cirkels kan worden bepaald met de formule $$x={{d^2-r^2+R^2} \over 2d}$$
(uitleg)
Stel cirkel met centrum O en straal 1.
Straal van kleine cirkel met centrum E is r; de straal R van de cirkel met centrum A, is dan 2-r. De afstand d tussen beide centra is ook 2-r. Ingevuld in de bovenstaande formule geeft dat de volgende vergelijking: $$ x={{(2-r)^2 -r^2+(2-r)^2} \over 2\cdotp(2-r)}$$ Maar in dit geval is x gelijk aan 1 (want gelijk aan x-waarde van O) wat, vereenvoudigd, de volgende vergelijking oplevert: $$ 1={{2(2-r)^2 -r^2} \over 2 \cdotp (2-r)}$$ De wortels zijn \( r= 3 +\sqrt 5\) en \( r= 3 -\sqrt 5\). AB wordt in dit geval door E gedeeld in \(AE={2-(3+\sqrt 5)}={ \sqrt 5-1}\) en \(EB=3 – \sqrt 5\). De gulden snede verhouding geldt als $${AE \over EB} ={AB \over AE}$$ Dus: $${{\sqrt 5-1}\over{3-\sqrt 5}}={2 \over {\sqrt5 -1 }} $$ en  vereenvoudigd:
$$6-2\sqrt5=6-2 \sqrt5$$ Dus E verdeelt AB in de verhouding van de gulden snede als het snijpunt van cirkels met centrum E en A exact op de diameter loodrecht op AB valt. QED.

11 juli 2018  
, , , ,