R nul
The basic reproduction ratio (or number) R0 is arguably the most important quantity in the study of epidemics and notably in comparing population dynamical effects of control strategies. The quantity is defined as the expected number of new cases of an infection caused by a typical infected individual in a population consisting of susceptibles only. In the last 10-15 years R0 is an ingredient in almost all papers that use some mathematical modelling in studying the spread of infectious agents.
Uitgangspunten
Prima, we moeten dus vooral letten op het basisreproductie getal, R0. Maar hoe kom je precies aan dat reproductiegetal? Hoe wordt het berekend? Om dat te begrijpen moeten we kijken naar drie factoren die de dynamiek van een epidemie bepalen: overdraagbaarheid van het virus, contactfrequentie van ontvankelijken of potentiële dragers en duur van besmettelijkheid.
- De overdraagbaarheid
waarschijnlijkheid van transmissie bij contact tussen geïnfecteerd persoon en ontvankelijk persoon van het virus noemen we q - de gemiddelde contactfrequentie
tussen geïnfecteerden en ontvankelijken geven we weer met c̄ - en de gemiddelde duur van de besmettelijkheid noemen we T.
Op grond van deze factoren is definiëren we het reproductiegetal R als volgt: \( q \times \overline{c} \times T \).
De effectieve overdrachtssnelheid is het resultaat van de combinatie van de overdraagbaarheid en de gemiddelde contactfrequentie. Het wordt aangeduid met een extra symbool: \(\beta= q \times \overline{c}\).
De snelheid waarmee het aantal geïnfecteerden afneemt is omgekeerd evenredig met de duur van de besmettelijkheid. Voorbeeld: Na één dag zijn er van de 1000 geïnfecteerden bij een herstel van 10 dagen nog \(1000 – {1000 \over 10} = 900\) over. Na 10 dagen is iedereen hersteld. Dus de snelheid v waarmee het aantal besmette “dragers” afneemt is dus \(v=\frac{1}{T} \) (wat op hetzelfde neerkomt als \(T=\frac{1}{v} \))
Een epidemie komt op gang
Het verloop van een epidemie kan nu worden nagebootst met een veelgebruikt model (SIR). Hierin wordt de totale bevolking (N) verdeeld in drie groepen: degenen die nog niet ziek zijn geweest (S van susceptible), de geïnfecteerden (I) en degenen die zijn hersteld of overleden (R van removed, voor de optimisten recovered); met andere woorden: N = S + I + R.
De verhouding waarmee ze in de bevolking voorkomen geven we als volgt weer: s = S/N, i=I/N en r=R/N.
De veranderingen per tijdseenheid zijn te vangen in drie vergelijkingen:
- \(\frac{dS}{dt} = – \beta {S \times I \over N}\) (afname aantal ontvankelijke personen vanwege ziekte) -als fracties: \(\frac{ds}{dt} = – \beta si\)
- \(\frac{dI}{dt} = \beta {S \times I \over N} – vI\) (verandering aantal geïnfecteerden: toename besmette personen – aantal personen dat hersteld of overlijdt) -als fracties: \(\frac{di}{dt} = \beta si – vi\)
- \(\frac{dR}{dt} = vI\) (verandering herstelden/overledenen) -als fracties:\(\frac{dr}{dt} = vi\)
Wanneer ontstaat er nu een epidemie? Het antwoord kunnen we nu geven: Als het aantal geïnfecteerden groeit; dus als er meer mensen besmet raken dan er weer beter worden. In termen van het model, als \(\frac{di}{dt} > 0\). En op basis van 2 kunnen we dit ook schrijven als: \(\beta si – vi>0\).
Nu wat eenvoudige algebra. Breng vi achter het groter-dan-teken: \(\beta si >vi\) en deel vervolgens beide zijden door v: \(\frac{\beta si}{v} > i\). Omdat nu aan beide zijden nog i staat kunnen we die ook via delen wegwerken. Wat dan resteert is \(\frac{\beta s}{v} > 1\)
In het allereerste begin van een epidemie is de gehele bevolking (minus de besmettingshaard) ervoor bevattelijk; dus \(s \approx 1\). Ziehier, de oorspronkelijke, primordiale reproductieverhouding: R0 = \(\frac{\beta}{v}\) en die moet groter zijn dan 1 wil er een epidemie op gang komen:
\(\frac{\beta}{v} > 1\)
Substitueren we v en \(\beta\) met hun uitgangswaarden (\(\beta= q \times \overline{c}\) en \(v=\frac{1}{T} \)) dan resulteert
\( q \times \overline{c} \times T > 1 \) .
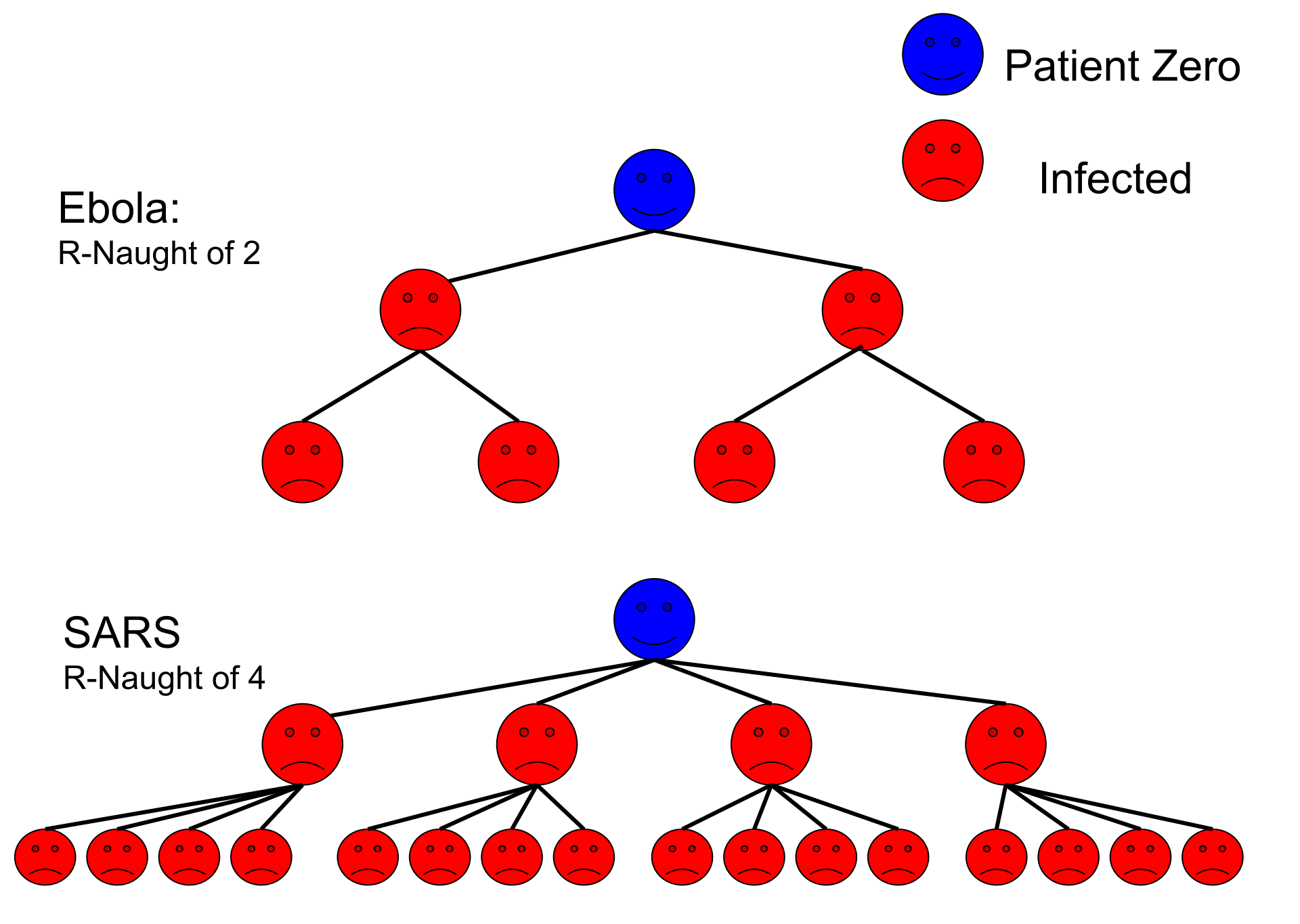
Na wat modelleren en enig rekenwerk stellen we dus vast dat, in spreektaal uitgedrukt, een epidemie op gang komt als één persoon meer dan één andere persoon besmet. De mazelen heeft een R0 groter dan 12, de bof groter dan 4. Van het coronavirus is het onbekend en de schattingen lopen flink uiteen, maar reëel lijkt een schatting tussen 2 en 3 (de R0 van SARS was iets hoger dan 3).
Omdat besmettelijkheid en duur van de ziekte de biologische kenmerken van de ziekte zijn waarover zeker in de beginfase van een nieuwe epidemie weinig bekend is en ook weinig kan worden gesleuteld, blijft voor de beïnvloeding van het verloop van een epidemie alleen de gemiddelde contactfrequentie c̄ over. Dit is dus de reden van “houd (anderhalve meter) afstand” en “blijf thuis”!
Toegift. R effectief
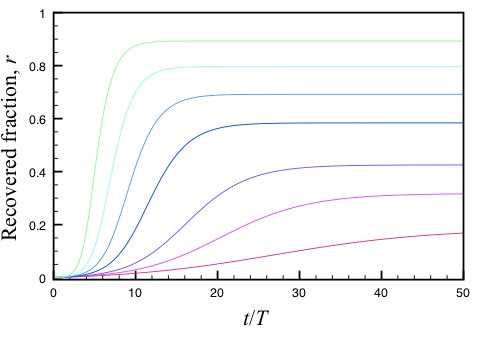
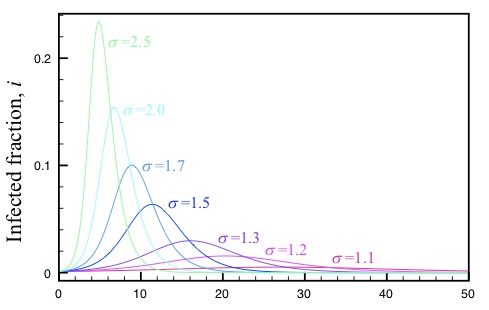
Hoe verloopt een epidemie bij verschillende effectieve overdrachtssnelheden? De R0 gaat dan over in R1, R2, kortom Re , het effectieve reproductiegetal, want er komen minder ontvankelijken (op weg naar kudde-immuniteit)
Het tijdverloop t kunnen we in samenhang (normaliseren) brengen met de duur van de besmettelijkheid T, \(\tau = t/T\). De hierboven gepresenteerde vergelijkingen komen er dan als volgt uit te zien:
\(s =1 – i – r\)
\(\frac{di}{d\tau} = \beta (1 – i – r) i – i\)
\(\frac{dr}{d\tau} = i\)
Met behulp van dit model en de initiële condities \(t=0, r=0, i\ll 1\), kunnen de volgende verloopsscenario’s worden gevonden voor de verschillende overdrachtssnelheden (hier \(\sigma\) gedoopt):