Het mesolabium, temperamenten en Descartes’ passers

In het oude Griekenland hadden de Deliers te kampen met een plaag. Ten einde raad riepen ze de hulp in van de goden. Het orakel voorspelde dat de plaag zou verdwijnen als zij een altaar zouden maken dat twee keer zo groot was als hun huidige altaar. De werklieden wisten niet hoe ze dat voor elkaar konden krijgen en de Deliers gingen naar Plato voor advies. Die wees hen erop dat de god helemaal geen dubbel zo groot altaar wilde; Apollo had de Deliers er slechts op willen wijzen dat zij de wiskunde ernstig hadden verwaarloosd.

Hoe verdubbel je een kubus (of een andere driedimensionale vorm)? Hippocrates van Chios (rond 430 v.Chr) had aangetoond dat het probleem van de verdubbeling van een kubus kon worden opgelost met behulp van twee middelevenredige lijnen tussen twee gegeven lijnen: vindt, bij gegeven lijnen A en B, de lijnen X en Y zodat geldt: A:X=X:Y=Y:B¹.

Middelevenredigheden in de wiskunde

Maar hoe vind je die twee lijnen? Het is één van de drie klassieke meetkunde problemen en velen hebben er zich de tanden op stukgebeten. Volgens Eutocius van Ascalon (6de eeuw AD) zijn er twaalf oplossingen bedacht². Met alleen passer en lineaal is het probleem namelijk niet op te lossen³; kegelsnedes en cylinders schenen soelaas te bieden. Maar Eratosthenes van Cyrene, een grieks wiskundige uit de derde eeuw voor Christus, vond dat allemaal veel te ingewikkeld:

Do not seek to do the difficult business of the cylinders of Archytas, or to cut the cones in the triads of Menaechmus⁴ , or to draw such a curved form of lines as is described by the god-fearing Eudoxus.

Hij kwam met een mechanische oplossing die in zijn ogen dus verreweg het eenvoudigst was en die Eutocius het mesolabium noemde. Tussen twee evenwijdige lijnen bevinden zich drie gelijkvorminge driehoeken waarvan er twee -DEF en GHI- kunnen worden verschoven. AW is één van de gegeven lijnen en RI is de tweede lijn afgetekend op HI. Verschuif de driehoeken zodanig dat P, Q en R op de lijn AS komen te liggen en RI:QF=QF:PC=PC:AW.

Deze handige oplossing raakte niet in het vergeetboekje, omdat Pappos van Alexandrië (vierde eeuw na Christus) haar opnam in zijn fameuse verzameling van wiskundige problemen (Synagoge; latijn Collectiones). Ook bij handwerkers was het instrument bekend. Vitruvius noemt het in boek IX van zijn De Architectura als één van de ontdekkingen waaraan de mensheid meer te danken heeft dan aan de sportieve prestaties van de olympische winnaars; die kregen daar in zijn ogen onevenredig veel lof voor toegezwaaid.

Temperament en Musica scientia

In het midden van de 16de eeuw duikt het mesolabium weer op, maar nu in de musica scientia; die was op zoek naar een uitbreiding van haar pythagoreïsche grondslag. Dat ging als volgt.
Pythagoras had met zijn leer van de eenvoudige getalsverhoudigen van octaaf (1:2) en kwint (2:3) de grondsteen van de muziektheorie gelegd. De diatonische toonreeks⁵ bleek uit deze twee verhoudingen te kunnen worden opgebouwd en muziek kreeg daarmee een mathematisch grondslag. Maar niet niet de muziek, de hele kosmos zou volgens de Pythagoreërs berusten op eenvoudige getalsverhoudingen waarmee zelfs een “muziek van de sferen” werd voortbracht. De pythagoreïsche muziektheorie kreeg overigens al in de antieken weerwoord van onder meer Aristoxenus, die niet zo gecharmeerd was van dit mathematische keurslijf en liever op het gehoor vertrouwde.

Toen in de Middeleeuwen de muziek een polyfone richting insloeg en ook de reine grote terts (4/5) en sext (3/5) als consonant⁶ werden beschouwd, bleek dat een aantal eigenschappen van het pythagoreïsche toonsysteem op gespannen voet stonden met deze meerstemmige muziek.

1.  gaat men twaalf kwinten omhoog en vervolgens 7 octaven naar beneden, dan landt men niet op dezelfde toon, maar zit er net iets naast: de pythagoreïsche komma. Dat verschil is een gevolg van de wederzijdse onverenigbaarheid van de consonanten⁷ 
2. de pythagorese grote tertsen zijn iets kleiner dan de reine grote terts⁸
3. De melodie: C -G -D -A -E -C, geheel uitgevoerd in reine intervallen, eindigt niet op de C waarmee is begonnen, maar op een C die een syntonische komma hoger is. Het toonsysteem met louter reine intervallen is dus instabiel.

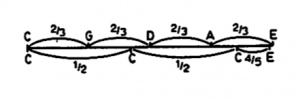
De zangstem heeft de flexibiliteit om de intervallen tijdens de uitvoering iets groter of kleiner te maken, maar bij orgel- of klavecimbeluitvoeringen bestaat die mogelijkheid niet; de stemming ligt vast. Om de gerezen problemen het hoofd te bieden begonnen de instrumentenbouwers te “temperen”. Omdat een reeks van vier kwinten van C naar E een syntonische komma groter is dan de reeks van twee octaven en een reine terts (zie bovenstaande figuur), werd dit vereffend door de kwinten te temperen met een kwart van de syntonische komma. Deze stemming met reine octaven, tertsen en sexten had nog een voordeel: er is maar één hele toon. Die is middelevenredig -het duurde even maar we zijn terug bij het thema- tussen de reine grote en kleine toon, dus tussen 8/9 en 9/10. Hieraan heeft dit stemsysteem ook zijn naam te danken: middentoonstemming.
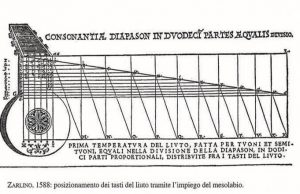
Er was dus behoefte aan het bepalen van middelevenredigheden en Gioseffo Zarlino, die zelf een systeem voorstelde waarbij 2/7 komma over twaalf tonen werd verdeeld, wist dat daar al lang geleden een handige methode voor was ontwikkeld: In zijn Institutione harmonichi (1558) verwoordde hij dat als volgt.

The other method of dividing the consonances, in two, or in so many parts one wants, being equal, is not only beautiful: but also more useful then the preceding, for being more universal; and it was discovered by Eratosthenes, when he found the duplication of the cube, at the time when the Dalij (as Johannes Philoponus [Giovanni Grammatico] narrates) were troubled by the plague; the same invention, together with many others, Giorgio Valla from Piacenza put in the “Fourth book of the Geometry”, teaching how to find two middle lines between the given two. It is well true, that without the help of an instrument, something called a mesolabium, whatever effort would be vain and useless; but before I go more ahead, I will show the way to build the instrument; and then I will teach how to find the lines.⁹

Dankzij de muziek stond het mesolabium weer in de belangstelling.

Ook Franscisco de Salines greep bij de constructie van zijn middentoonsysteem in 1577 terug op het mesolabium (dat hij ten onrechte toeschreef aan Archimedes). Daarbij moest hij namelijk de D en E zien te vinden in de tritonus C-F#. Dat, zo merkte hij op,

will be very easy to those who know the use of a certain instrument invented by Archimedes, which is called mesolabium, from finding mean lines by it.¹⁰

Als eerste stelt Salinas voor ook bij de gelijkzwevende stemming het mesolabium te gebruiken: deel het octaaf onder in twaalf evenredige tonen met behulp van het mesolabium¹¹.

‘We judge this one thing must be observed by makers of viols, namely, that the octave must be divided into 12 parts equally proportional, which 12 will be the equal semitones. And since they cannot accomplish this by the 9th of the 6th book [the mean proportional construction] or by any other proposition of Euclid, it will be the task to use the instrument which we said was called the mesolabium, invented (as they believe) by Archimedes: by which they will be able to obtain a line divided into as many equal parts as they wish. We have not bothered to append the rule of its construction here, because mention is made of its principle by Vitruvius in his 9th book on architecture; from whom and from his expositors they will be able to obtain the method of constructing it: for it is to practical men for framing mqst matters not only useful, but well-nigh indispensible.¹²

Wat Salinas voorstelde is bepaald niet eenvoudig: met twaalf driehoeken in het mesolabium gaan schuiven tot uiteindelijk alles mooi op een lijn ligt. Maar voor luitbouwers bood het natuurlijk wel een uitkomst om de fretten mooi op de toets te plaatsen. Later kwamen ook proportionaalpassers in zwang om bij de indeling de juiste verhoudingen te vinden.

Descartes’ passers en zijn nieuwe wetenschap

Descartes’ eerste werk, Compendium musicae uit 1619, was een nieuwjaarsgeschenk aan zijn vriend Isaac Beeckman en ging over muziek. Hij verwijst er één keer naar Zarlino, maar we mogen ervan uitgaan dat hij zijn werk goed gekend zal hebben. Het toonstelsel, zo vond Descartes, moest gebaseerd zijn op eenvoudige rekenkundige verhoudingen; irrationele getallen waren dus uitgesloten.¹³  Descartes liet het temperen links liggen en opteerde voor een reine stemming.

Bij de opdeling van het octaaf ging hij heel inventief te werk. Hij nam als uitgangspunt de lijn AB die hij in C in tweeën deelde: het octaaf.

Deze procedure herhaalde hij telkens opnieuw: CB in D (kwint); dan CD in E “waaruit direct de grote tests wordt gevormd (met verhouding (4:5), en indirect alle andere consonanten. Het is niet nodig CE nog verder te verdelen.”¹⁴ Een mesolabium had Descartes hier niet voor nodig!

Tussen november 1618 en april 1619 gingen Descartes en Isaac Beeckman heel vriendschappelijk met elkaar om en onderzochten zij gezamenlijk allerlei fysische en mathematische problemen. Op 26 maart 1619 schreef Descartes aan Beeckman dat hij er met zijn passers er in was geslaagd verschillende vormen van derdegraads vergelijkingen op te lossen. Zes dagen eerder was hij teruggekomen van een bezoek aan Beeckman in Middelburg en in de tussenliggende periode had hij “zijn muze ijveriger dan ooit gecultiveerd”¹⁵. Vermoedelijk kende Beeckman die passers zodat het hem wel duidelijk was waarmee Descartes op dat moment bezig was.
Pas midden 19de eeuw zijn notitieboeken van Descartes uit die tijd als Cogitationes Privatae weer boven water gekomen en weten we welke passers hij bedoelde. Er zijn daarin namelijk ongedateerde aantekeningen te vinden waarin hij het heeft over passers om derdegraadsvergelijkingen op te lossen. In dat verband gebruikt hij ook de aanduiding “lijn van de mesolabiumpasser”.¹⁶ Er staat een tekening bij die zonder verdere toelichting ook niet veel verder helpt. Gelukkig gebruikte Descartes dit idee bijna twintig jaar later opnieuw in zijn Geométrie uit 1637 en geeft er dan wel een goede beschrijving van. Maar nu hij laat de benaming mesolabium achterwege, presenteert het als een instrument om middelevenredige lijnen voort te brengen en heeft het niet meer over het oplossen van derdegraads vergelijkingen met dit instrument.

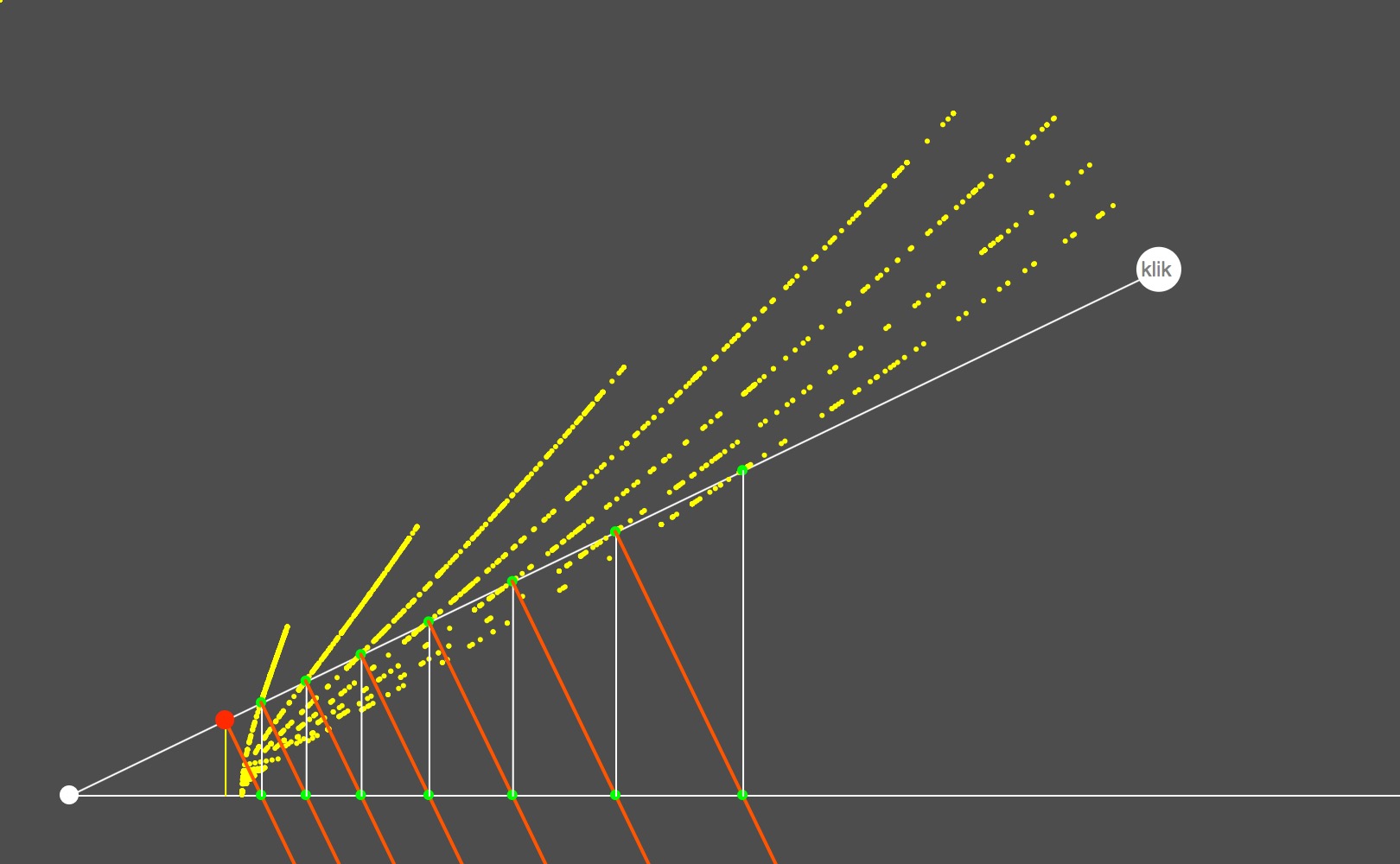
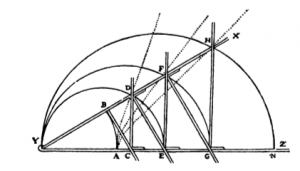
Descartes’ mesolabium maakte iets mogelijk waarover men tot dan toe alleen had gedroomd: met één beweging een scala van middelevenredige lijnen genereren; ze komen als het ware uit het niets tevoorschijn.¹⁷ De werking is als volgt: als de benen YX en YZ van de passer zijn samengeklapt, vallen B en de verschuifbare punten D, F en H samen. Zij bevinden zich in de uitgangspositie allen in A, met BC, DE, FG over elkaar heen naar beneden gericht. Wanneer de passer zich opent, duwen BC, DE, FE etc. CD, EF, GH etc. naar rechts waardoor YD, YF en YH proportioneel toenemen.
Zo onstaan congruente rechthoekige driehoeken YBC, YCD, YDE, YEF etc. waarvoor geldt: YB:YC=YC:YD=YD:YE=YE:YF etc.¹⁸

In het model hieronder begint de reeks bij de gele lijn onder de rode punt en eindigt in dit voorbeeld bij de zevende evenredige lijn. Naar de curves die ontstaan door de gele puntjes verwees Descartes met de aanduiding “lijn van de mesolabiumpasser”.

Twee kenmerken zijn nog het vermelden waard: YC kan alle waarden groter dan YA (=YB) aannemen en in een numerieke interpretatie, waarin YA=YB=1 en YC=X geldt de volgende proportionaliteit: 1:X=X:X²=X²:X³ etc.

Met behulp van de officiele versie in de Geométrie is duidelijk geworden wat Descartes bedoelde met zijn mesolabische passer. Dan rest nog de vraag hoe hij op het idee is gekomen. Descartes, opgeleid aan het Jezuïtencollege van La Fleche, zou inspiratie gevonden kunnen hebben in Christoph Clavius’ becommentarieerde uitgave van Euclides’ Elementen uit 1589¹⁹. Deze uit Bamberg afkomstige jezuiet werd gezien als de parel van de orde. Clavius’ Algebra uit 1607 was vermaard en zijn becommentarieerde uitgave van Euclides Elementen is tot in de 18de eeuw gedrukt. Descartes kende zijn werk goed en zijn kennis van algebra was volgens eigen zeggen toen nog geheel gebaseerd op Clavius’ werk.²⁰

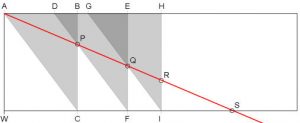
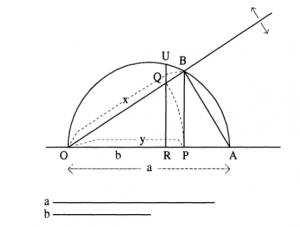 In het commentaar op Euclides gaat Clavius in op de constructie van middelevenredigheden en stelt een constructie voor die bijna geometrisch is²¹ (dw.z. een constructie met passer en lineaal die hoger werd gewaardeerd dan de mechanische werkwijze van Eratosthenes). Trek een cirkel met diameter OA (=a). Neem OR = b. Trek loodrecht op OA RU. Neem een lineaal en leg die over O. Die snijdt de cirkel in B en UR in Q. Beweeg de lineaal met als draaipunt O zo, dat OQ=OP (eigenlijk vormen OPQ een cirkel met centrum O en straal OP). De gezochte middelevenredigheden zijn dan OB (x) en OP (y).

Omdat Clavius in zijn werk de term mesolabium nergens vermeld, zal Descartes de benaming waarschijnlijk uit de geschriften van de Zarlino hebben opgepikt²². Omdat de curve die hij ermee aanduidde geen directe functie heeft in het oplossen van de derdegraads vergelijking is het niet onredelijk te veronderstellen²³ dat Descartes zijn mesolabische passer had ontwikkeld voor de constructie van middelevenredige lijnen en pas daarna op het idee kwam dat er ook derdegraads vergelijkingen mee konden worden opgelost.
Hoe? Descartes gaf zelf het voorbeeld van de vergelijking x³=x+2. Door zijn mesolabische -of proportionele- passer zover open te klappen dat een bepaald lijnstuk (CE) gelijk was aan 2 kon de oplossing kon worden afgelezen van een ander lijnstuk. Al rekenende met zijn passers moet hem op een bepaald moment het idee zijn ingevallen dat numerieke bewerkingen als optelen, aftrekken, vermenigvuldigen, delen en wortel trekken gerelateerd zijn aan meetkundige bewerkingen als één betrokken lijnsegment gelijk gesteld wordt aan 1. Met behulp van de proportieleer laat Descartes, heel veel later in de La Geométrie, zien hoe dat in zijn werk gaat.

Vermenigvuldigen: 1:a=b:ab;
Delen: a/b:1=a:b en
Worteltrekken: 1: √a=√a: a.

Zo verzachtte Descartes het harde onderscheid dat de Grieken na de ontdekking van de incommensurabiliteit hadden geïntroduceerd tussen het numerieke/discrete en het meetkundige/continue. Maar dat is bijna twintig jaar later. Wat hij waarschijnlijk slechts in grote contouren voor zich zag gaf hem voldoende vertrouwen Beeckman in zijjn brief van 26 maart 1619 te schrijven dat hij een nieuwe, allesomvattende, universele mathematica voor zich zag: “Laat ik open zijn over wat mij voor ogen staat. Wat ik mij voorstel is niet zoiets als Lull’s Ars Brevis, maar een geheel nieuwe wetenschap ²⁴, waarmee alle vraagstukken die ten aanzien van elke soort grootheid -zowel continu [meetkundig] als discreet [rekenkundig]- kunnen worden gesteld, op een universele manier zouden kunnen worden opgelost.”

Aan de muziektheorie ging Descartes’ mesolabische of proportionele passer, uiteindelijk niet onopgemerkt voorbij. Friedrich Marpurg. een verlichte muziekcriticus en -theoreticus, publiceerde in 1776 zijn Versuch über die musikalische Temperatur. Daarin adviseerde hij het gebruik van Descartes’ instrument. Wer Lust hat, die Construction einer gleichschwebenden Temperatur annoch auf eine andere Art zu versuchen, kann dazu der Methode des Cartesius bedienen, welcher vermittelst eines aus verschiednen Wnkelmassen bestehenden Instruments so viele Mittelproportionale, als man verlanget, zwischen zwey gegebnen Linien erfinden lehret, und wovon man unter andern auch die Geometrie des Paters Lamy, Seite 200.201. nachlesen kann.²⁵

. link vertalingen

1. We werken het algebraïsch uit, iets wat de Grieken nooit gedaan zouden hebben. Neem B=2A. Dan is A:X=X:Y=Y:2A.
   Werk uit: X²=AY en Y²=2AX.
   Om Y te vervangen in X²=AY kwadrateren;:
   X⁴ =A²Y². Vervang Y²:  X⁴=A² x 2AX;
   X⁴=2A³X.
   Ergo X³=2A³
   Dus een kubus met rib X is is twee keer zo groot als die met rib A ↩︎
2. Eutocius bespreekt ze in zijn commentaar op Archimedes’ Over de bol en cylinder. Van hem is ook de naam mesolabium afkomstig voor de constructie van Eratosthenes: griekse mesos: midden en labos=lambanein: nemen, pakken, grijpen) ↩︎
3. Euclides had laten zien dat voor het vinden van één middelevenredige lijn lineaal en passer wel voldoende zijn ↩︎
4. Ellips, hyperbool en parabool ↩︎
5. De reeks van hele toonintervallen c-d-e-f-g-a-b-c ↩︎
6. Ze hoefden niet te worden “opgelost” in een consonant en konden dus ook muzikaal belangrijke plaatsen als het slot worden gebruikt. Het duurde vervolgens niet lang totdat de tertsen de harmonie domineerden ↩︎
7. Mathematisch gesteld: 1/2⁷ is niet gelijk aan 2/3¹²; machten van verschillende priemgetallen kunnen nooit gelijk zijn. ↩︎
8. Bv. de grote terts C-E is dan 8/9 x8/9=64/81; de reine grote terts is 4/5. Het verschil 80/81 en heet syntonische komma. ↩︎
9. E altro modo di divide le Consonanze, in due, overo in quante partisi uoglia, che fiano equali, è non solamente bello; ma anco piu utile del primo ; per esser piu universale & su ritrovaro (come uogliono alcuni) da Archita, & altrida Eratosthene, quando ritrovò il Raddoppiamento del Cubo, nel tempo che i Dalij (come narra Giovan Grammatico) erano moestati dalla pestilenza; la quale Inventione & molt’altre insieme raccolse Gregorio Valla Piacentino nel Quarto libro della Geometria; insegnando di ritrovar Due mezame linee proportionali tra due proposte. E ben vero, che senza l’aiuto d’un Istrumento, nomina Mesolabio, farebbe uana & inutile ogni fatica: però avanti ch’io vada più oltra, mostraro il modo di fabricar l’instrumento, & dopoi insegnerò ritrovar le Linee..Liber Secona, cap. 24. Vertaling Leonardo Perretti op Tonalsoft ↩︎
10. quoad facilimum erit scientibus usum cuiusdam instrumenti ab Archimede inventi, quod Mesolabium, a medijs sumen dis lineis ..
    De musica libri VII, 1577, blz. 147 ↩︎
11. Neem A als grondtoon en B als octaaf. Vind nu X1, X2, X3 .. X11 zodat A: X1=X1:X2=X2:X3=X3:X4 …X10:X11=X11:B. Het gaat dus om 11 “midden evenredigheden” tussen A en B. ↩︎
12. De musica libri VII, 1577, blz. 173 ↩︎
13. Hier uitte zich al Descartes voorliefde voor clair et distinct. “Deze verhouding moet rekenkundig zijn en niet meetkundig. De reden daarvoor is dat er dan niet zoveel dingen op te merken zijn, omdat de verschillen steeds gelijk zijn. En dus wordt het zintuig niet zo gauw vermoeid, zodat het alles duidelijk kan onderscheiden.” en “Het object moet zodanig zijn dat het door het zintuig niet te moeilijk of te onduidelijk wordt waargenomen.” Bibliotheek Descartes, Bd.1, blz.87, 86 ↩︎
14. Bibliotheek Descartes Bd.1., blz. 99. ↩︎
15. ubi Musas meas diligentiùs excolui quàm unquam hactenus ↩︎
16. linea circini-mesolabi. Bibliotheek Descartes Bd.1, blz. 184. ↩︎
17. je ne croy pas qu’il y ait aucune façon plus facile, pour trouver autant de moyens proportionelles qu’on veut ny dont la demonstration soit plus evidente que d’y employer les lignes courbes qui se descrivent par l’instrument XYZ cy desses expliqué. Oeuvres de Descartes, ed. Adam & Tannery, Bd. 6, blz. 442 ↩︎
18. De verdubbeling van de kubus los je op door de passer zo ver open te schuiven dat YE=2 x YB. De gezochte lengte van de ribbe van de kubus die twee keer zo groot is, is dan YC. ↩︎
19. Euclidis elementorum libri XV accessit XVI de solidorum regularium cuiuslibet comparatione. Het is een suggestie van Henk Bos in Redefining Geometrical Exactness, blz 74 ↩︎
20. Tegen de wiskundige John Pell vertelde hij in 1646 dat hij al 30 jaar geleden Clavius’ Algebra had gelezen. He says he had no other instructor for Algebra than ye reading of Clavy Algebra above 30 yeares ago. Helen Hervey, Hobbes and Descartes in the Light of Some Unpublished Letters of the Correspondence between Sir Charles Cavendish and Dr. John Pell, Osiris, Vol. 10 (1952), blz 78
    Aan Mersenne schreef Descartes in 1629 iets over de kwadratrix en verwees naar Clavius commentaar op Euclides: pource qu’elle sert a quarrer le cercle & mesme a diviser l’angle en toutes sortes de parties esgales aussy bien que celle cy & a beaucoup d’autres usages que vous pourrés voir dans les elemans d’Euclide commantés par Clavius. ↩︎
21. Ex his sine magno labore inter duas rectas datas reperiemus duas medias proportionales, non quidem geometriee omnino, sed quasi attentando et praxim ipsam iterum atque iterum repetendo, donee id, quod quaerimus, assequamur. ↩︎
22. We gaan ervan uit dat Descartes toen Pappus Collectiones nog niet kende. Zie vorige noot. ↩︎
23. Henk Bos, Redefining Geometrical Exactness, blz 239, noot 22 en Sasaki, C, Descartes’ mathematical thought, blz. 119 ↩︎
24. scientiam penitus novam, AT. X. blz. 157 ↩︎
25. Par 174, blz. 150 ↩︎