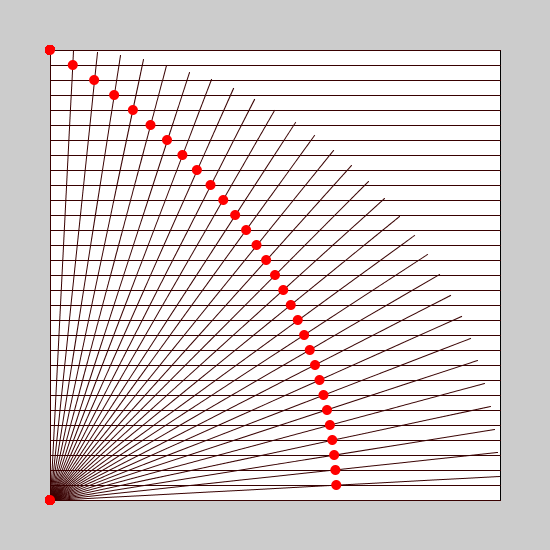
Quadratrix van Hippias

Sinds de oude Grieken hebben drie problemen de mathematici gefascineerd: de kwadratuur van de cirkel, de verdubbeling van de kubus en de driedeling van een gegeven hoek.

Zijn er oplossingen voor? De Grieken waren na enige tijd tot de conclusie gekomen dat deze vraagstukken niet konden worden opgelost met louter passer en lineaal. Daarom werd er ook gekeken naar speciale curves waarmee de gestelde opgaves toch konden worden opgelost. Eén van die curves is de quadratrix van Hippias van Elis. Rond 420 voor Chr. bedacht hij deze curve met als doel een oplossing te vinden voor de driedeling van een gegeven hoek.

De quadratrix is een curve die alleen kan worden geconstrueerd met behulp van beweging en die gaat als volgt: De straal van een cirkel draait van A naar S over een hoek van 90 graden en in deze tijdspanne daalt een horizontale lijn AB naar beneden tot OS. Op elk moment snijdt de horizontale lijn de straal en die verzameling snijpunten vormt de gezochte quadratrix.

Quadratrix (klik op figuur voor beweging)

var center;
var Xoff=30;
var breedte=350;
var t=0;
var motion=false;
var arrSnijpunten = [];
var onderbreek=false;

function setup() {
  cnv=createCanvas(breedte+2*Xoff, breedte+2*Xoff);
  colorMode(HSB, 90);
  strokeWeight(1);
  center = createVector(Xoff, height-Xoff);
}

function draw() {
  if (onderbreek===false) {
    tekst('O', center.x-15, center.y+18, 18);
    tekst('A', center.x-15, Xoff, 18);
    tekst('B', center.x+breedte+5, Xoff, 18);
    tekst('S', center.x+breedte+5, center.y+18, 18);
    if (motion) {
      stroke(0);
      background(255);
      tekst('O', center.x-15, center.y+18, 18);
      tekst('A', center.x-15, Xoff, 18);
      tekst('B', center.x+breedte+5, Xoff, 18);
      tekst('S', center.x+breedte+5, center.y+18, 18);
      rect(Xoff, Xoff, breedte, breedte);
      arc(center.x, center.y, 2*breedte, 2*breedte, PI+HALF_PI, TWO_PI);
      
      for (var i=0; i<arrSnijpunten.length; i++) {
        arrSnijpunten[i].tonen(3);
      }
      var LijnStart;
      var LijnEinde;
      var counter=t%270;
      if (counter<=90) {
        stroke(0, 200, 20);
        line(Xoff+breedte/2,Xoff,Xoff+breedte/2,Xoff+breedte);
        line(Xoff, Xoff+breedte/2,Xoff+breedte,Xoff+breedte/2);
        x = center.x + cos(radians(counter+270))*breedte;
        y = center.y + sin(radians(counter+270))*breedte;
        x1 = center.x + cos(radians(counter+270))*(breedte+150);
        y1 = center.y + sin(radians(counter+270))*(breedte+150);
        line(center.x, center.y, x, y);
        strokeWeight(3);
        line(x, y, x1, y1);
        strokeWeight(1);
        LijnStart=createVector(center.x, (breedte)/90*counter+Xoff);
        LijnEinde =createVector(breedte, (breedte)/90*counter+Xoff);
        line(LijnStart.x, LijnStart.y, LijnEinde.x+Xoff, LijnEinde.y);
        var Snijpunt=lineLine(center.x, center.y, x, y, LijnStart.x, LijnStart.y, LijnEinde.x, LijnEinde.y);
        //print(Snijpunt);
        if (Snijpunt!=false) {
          Snijpunt.tonen(3);
          arrSnijpunten.push(Snijpunt);
        };
        
        t+=0.3;
      } else {
        arrSnijpunten=[];
        t+=150;
      }
    } else {
      var teller=0;
      textSize(22);
      text('Oooo', Xoff-10, Xoff-10);
      for (var i = 270; i <= 360; i+=3) {
        stroke(0, 200, 20);
        x = center.x + cos(radians(i))*breedte;
        y = center.y + sin(radians(i))*breedte;
        line(center.x, center.y, x, y);
        LijnStart=createVector(center.x, (breedte)/30*teller+Xoff);
        LijnEinde =createVector(breedte, (breedte)/30*teller+Xoff);
        //LijnEinde.y=breedte-(breedte)/30*teller+50;
        line(LijnStart.x, LijnStart.y, LijnEinde.x+Xoff, LijnEinde.y);
        if (teller>0) {
          var Snijpunt=lineLine(center.x, center.y, x, y, LijnStart.x, LijnStart.y, LijnEinde.x, LijnEinde.y);
          Snijpunt.tonen(8);
        }
        teller++;
      }
    }
  }
}

function lineLine( x1, y1, x2, y2, x3, y3, x4, y4) {
  // calculate the distance to intersection point
  var uA = ((x4-x3)*(y1-y3) - (y4-y3)*(x1-x3)) / ((y4-y3)*(x2-x1) - (x4-x3)*(y2-y1));
  var uB = ((x2-x1)*(y1-y3) - (y2-y1)*(x1-x3)) / ((y4-y3)*(x2-x1) - (x4-x3)*(y2-y1));

  // if uA and uB are between 0-1, lines are colliding
  if (uA >= 0 & uA <= 1 && uB >= 0 && uB <= 1) {
    // optionally, draw a circle where the lines meet
    var intersectionX = x1 + (uA * (x2-x1));
    var intersectionY = y1 + (uA * (y2-y1));
    noStroke();
    var ditSnijpunt= new Snijpunt(intersectionX, intersectionY);
    return ditSnijpunt;
  }
  return false;
}

function keyTyped() {
  if (key === 'o') {
    onderbreek = true;
  } else {
    onderbreek = false;
  }
  // uncomment to prevent any default behavior
  // return false;
}

function mouseClicked() {
  if (motion==false) {
    motion=true;
  } else {
    motion=false;
  }
  setup();
}

function Snijpunt(x, y) {
  this.x = x;
  this.y = y;

  this.tonen = function(diameter) {
    noStroke();
    fill(120, 200, 200);
    ellipse(this.x, this.y, diameter, diameter);
    fill(0, 0, 200);
  };
}

function tekst(tekst, x, y, size) {
  fill(50);
  textSize(size);
  text(tekst, x, y);
  fill(0, 0, 200);
}

 

 

 

 

De figuur is gemaakt met P5.js, de javascript versie van Processing